Si tengo que recomendar una web de actividades matemáticas mediante juegos, esa sería el magnífico blog Juegos y matemáticas de Ana García Azcarate . Sirvan estas líneas de agradecimiento por tan fantástico trabajo.
El caso es que muchas de esas actividades están hechas con Tarsia. Por ejemplo: este
Buscando en Github alguna alternativa a Tarsia que fuera libre y que pudiera ejecutar en GNU-Linux, me topé con Jigsaw-generator de Julian Gilbey. ¡Muchas gracias, Julian!
Este es un ejemplo del aspecto que tienen los puzzles generados. Este en concreto se ha sacado de un ejemplo que el autor tiene colgado en el repositorio de la aplicación:
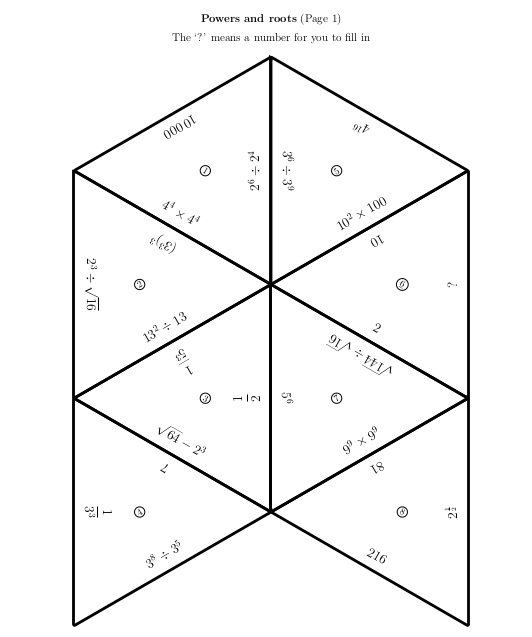
Vamos a ver cómo se instala y como se usa:
Instalando Jigsaw-generator de Julian Gilbey
Prerrequisitos
En el archivo INSTALL del repositorio indica qué es necesario tener instalado:
- Python 3.x (¿A qué estás esperando si todavía no usas Python?)
- Una distribución $\TeX$ ($\LaTeX$)
- Y el módulo PyYaml para manejar ficheros Yaml
Podemos instalar el módulo PyYaml con el siguiente comando:
sudo -H pip3 install PyYAML
Instalación propiamente dicha
Se da por descontado que has descargado el repositorio de la aplicación y que la ruta de trabajo apunta a esa carpeta.
Tal como pone en INSTALL ,solo hay que ejecutar los típicos:
./configure
make
sudo make install
Si todo va bien hará la instalación sin errores
Uso básico
El comando que genera el puzzle es:
Si lo ejecutamos sin ningún parámetro devolverá lo siguiente:
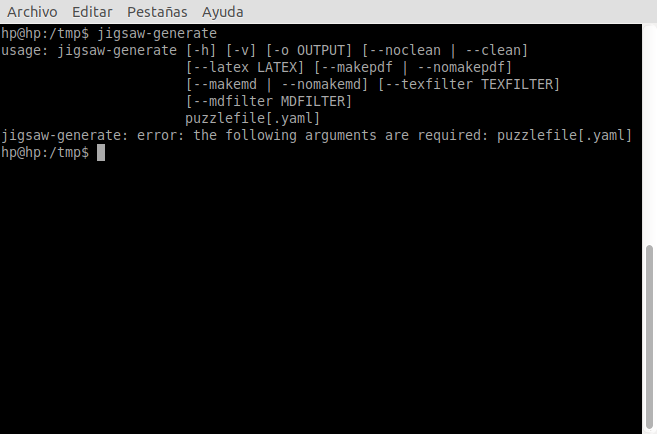
El error que nos da indica que necesitamos pasarle un fichero .yaml con toda la información del puzzle:
Veamos el ejemplo que corresponde con la imagen del puzzle que hemos visto antes y que aparece en el repositorio del autor:
# A hexagonal jigsaw puzzle, from http://www.mrbartonmaths.com/jigsaw.htm
format: 1
type: hexagon
title: Powers and roots
note: "The `?' means a number for you to fill in"
pairs:
- ['$10^6\div10^3$', '$1000$']
- ['$10^{23}\div10^{21}$', '$100$']
- ['$9^4\times9^5$', '$9^9$']
- ['$(3^2)^2$', '$81$']
- ['$6\times6^2$', '$216$']
- ['$2^4\div2^6$', '$\dfrac{1}{4}$']
- - '$4^2\times4$'
- puzzletext: '?'
solutiontext: '$64$'
- ['$2^6\times2$', '$128$']
- ['$23.1^0$', '$1$']
- ['$3^3\times3^3$', '$3^6$']
- ['$\sqrt{64}-2^3$', '$0$']
- ['$\dfrac{1}{5^2}\times\dfrac{1}{5}$', '$\dfrac{1}{5^3}$']
- ['$5^2\div5^4$', '$\dfrac{1}{5^2}$']
- ['$3^2\times3^3$', '$3^5$']
- ['$(3^3)^3$', '$3^9$']
- ['$2^3\div\sqrt{16}$', '$2$']
- - '$2^6\div2^4$'
- puzzletext: '?'
solutiontext: '$4$'
- ['$4^4\times4^4$', '$4^8$']
- ['$\sqrt{49}$', '$7$']
- ['$\sqrt{25}\times\sqrt{36}$', '$30$']
- ['$\sqrt{144}\div\sqrt{16}$', '$3$']
- ['$2^3\div2^4$', '$\dfrac{1}{2}$']
- ['$2\times2^2\times2^2$', '$32$']
- ['$10^2\times100$', '$10\,000$']
- ['$3^6\div3^9$', '$\dfrac{1}{3^3}$']
- ['$3^8\div3^5$', '$3^3$']
- ['$5^5\div5\times5^2$', '$5^6$']
- ['$9^9\times9^9$', '$9^{18}$']
- ['$(9^9)^9$', '$9^{81}$']
- ['$(4^4)^4$', '$4^{16}$']
edges:
- '$-1$'
- '$10$'
- '$13^2\div13$'
- '$39$'
- '$13^3$'
- '$108$'
- '$\dfrac{1}{2}$'
- '$\sqrt{128}$'
- '$\sqrt{20}$'
- '$2^{\frac{1}{2}}$'
- '$\dfrac{3}{2}$'
- '$9^{10}$'
El fichero yaml tiene una serie de campos:
- format: la versión del formato de archivo, debe tener 1 ya que solo hay una versión de la aplicación
- type: El tipo de rompecabezas que se está creando.
- smallhexagon, que consta de 6 triángulos
- hexagon, que consta de 24 triángulos
- triangle, que consiste en 16 triángulos más pequeños
- parquet, que consta de 4 cuadrados y 8 triángulos.
- title: Título
- puzzleTextSize o solutionTextSize: Tamaño del texto. Va de 0-9 siendo el 0 el más pequeño. Por defecto vale 5
- note: Subtítulo o nota explicativa arriba en la páginas
- pairs: Pares de ejercicio-solución. Se ponen entre corchetes y en código $\LaTeX$
- edges: Ejercicios que no se asocian a ninguna solución porque forman las esquinas del puzzle
Existen más opciones, para más detalle se remite a la documentación de la aplicación.
Ejemplo de uso
Vamos entonces a crear un puzzle sencillo:
El más sencillo es de tipo smallhexagon de 6 triángulos. Luego necesito 6 pairs y 6 edges. Creamos el fichero prueba_angulos.yaml:
type: smallhexagon
title: Radianes y grados
note: "Identifica ángulos iguales"
pairs:
- ['$0$','$0$']
- ['$90$','$\frac{\pi}{2}$']
- ['$180$','$\pi$']
- ['$270$','$\frac{3\pi}{2}$']
- ['$360$','$2\pi$']
- ['$45$','$\frac{\pi}{4}$']
edges:
- '$\frac{\pi}{6}$'
- '$\frac{2\pi}{6}$'
- '$\frac{\pi}{3}$'
- '$\frac{\pi}{5}$'
- '$\frac{5\pi}{6}$'
- '$\frac{2\pi}{6}$'
Solo nos queda ejecutar:
$ jigsaw-generate prueba_angulos.yaml
El resultado es:
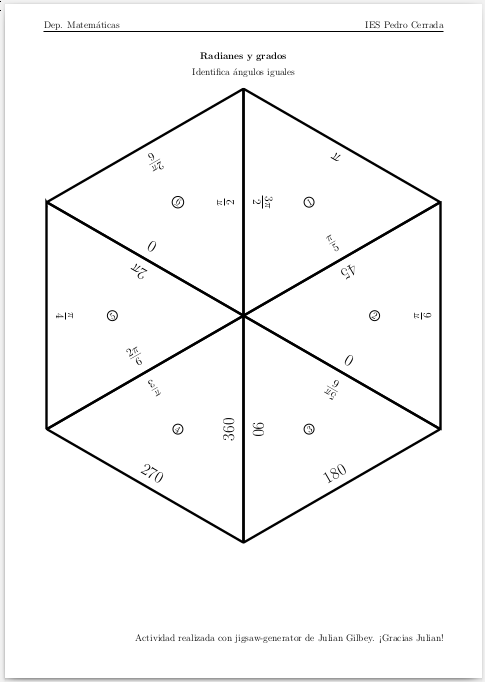
Y su solución:
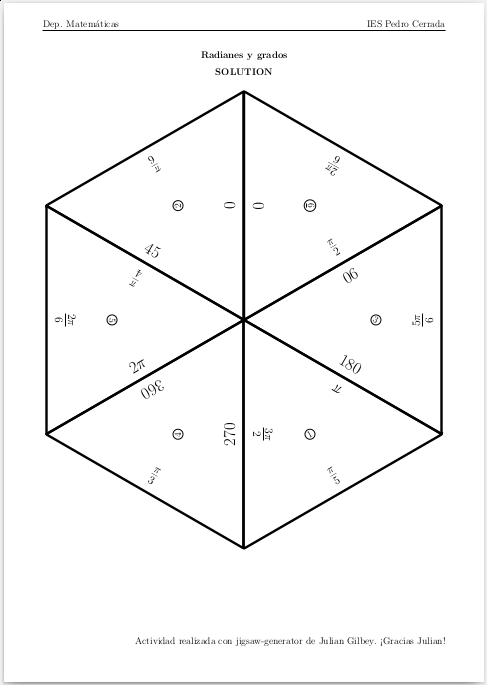
Y eso es todo. Como veis, en realidad, una vez instalado el programa solo hay que generar un fichero yaml con los datos y el tipo de puzzle.