Experimento aleatorio
Un experimento aleatorio o no determinista es aquél que si se repite varias veces no está garantizado obtener siempre el mismo resultado. Es decir, no se puede determinar cuál va a ser el resultado del experimiento hasta que no se realiza. En caso contrario, decimos que el experimento es determinista
Un experimento es aleatorio cuando depende de muchos factores y cualquier pequeña modificación de alguno implica obtener un resultado diferente.
Ejemplos
- Aleatorio: Lanzar un dado y ver el resultado
- Determinista: Calcular el tiempo que tarda en caer un objeto al suelo desde una distancia determinada
Espacio muestral y sucesos
- Espacio muestral: Conjunto de los posibles resultados del experimento. Se denota: E
- Sucesos simples o elementales: Cualquiera de los elementos del espacio muestral
- Sucesos compuestos: Sucesos formados por varios simples.
- Suceso seguro: Suceso compuesto por los elementos del Espacio muestral. Se cumple siempre
- Suceso imposible: Cualquier suceso que no se cumpla nunca. Se denota con el símbolo: ⌀
- Suceso contrario: Si A es un suceso, $\overline{A}$ es el suceso contrario. Es aquel que se cumple cuando no se cumple A
Ejemplos
Lanzamos un dado y comprobamos la cara que sale.
- Espacio muestral: E = {1, 2, 3, 4, 5, 6}
- Sucesos simples o elementales: 1, 2, 3, 4, 5 ó 6
- Sucesos compuestos: A = {que salga par} = {2, 4, 6}
- Suceso seguro: E = {1, 2, 3, 4, 5, 6}
- Suceso imposible: ⌀ = {que salga mayor que 6}
- Suceso contrario: Si A = {que salga par} = {2, 4, 6}}, $\overline{A}=\lbrace que\ salga\ impar\rbrace=\lbrace1,3,5\rbrace$
Operaciones con sucesos y relaciones
- Unión: la unión de los sucesos A y B es aquel suceso que contiene a todos los elementos de A y a los de B. Se denota: A ∪ B
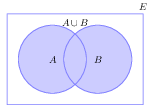
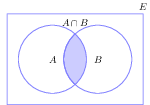
- Intersección: la intersección de los sucesos A y B es aquel suceso que contiene a todos los elementos que están tanto en A como en B. Se denota: A ∩ B
Ejemplos
Tomamos como experimento el resultado de lanzar un dado, y los sucesos:
| A = {que salga par} = {2, 4, 6} |
| B = {que sea mayor que 3} = {4, 5, 6} |
| C = {que salga impar} = {1, 3, 5} |
- A ∪ B = {2, 4, 5, 6}
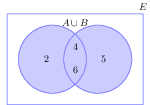
- A ∩ B = {4, 6}
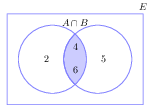
- A ∪ C = {1, 2, 3, 4, 5, 6} = E
- A ∩ C = ⌀
Compatibilidad de sucesos
Se dice que dos sucesos son incompatibles cuando su intersección es el conjunto vacío. En caso contrario se dice que son compatibles.
Ejemplo
En el ejemplo anterior, A y B son compatibles y A y C incompatibles.
Probabilidad en experimentos regulares y Regla de Laplace
Cuando todos los sucesos elementales de un espacio muestral finito están en las mismas condiciones de suceder se dice que son equiprobables, y al experimento se le llama regular.
Ejemplos de experimentos regulares
Lanzamiento de dados, monedas, extracción de cartas, …
Regla de Laplace
La probabilidad de un suceso de un experimento regular viene determinada por la Regla de Laplace:
$P(A)=\dfrac{Casos\ favorables}{Casos\ posibles}$
Ejemplo
Al lanzar un dado, los casos posibles son 6 ({1, 2, 3, 4, 5, 6}):
| La probabilidad de sacar un 3: $\lbrace3\rbrace\to \dfrac{1}{6}$ |
| La probabilidad de sacar par: $\lbrace2,4,6\rbrace\to\dfrac{3}{6}$ |
| La probabilidad de sacar más de 4: $\lbrace5,6\rbrace\to\dfrac{2}{6}$ |
Propiedades de la probabilidad
La probabilidad de un experimento regular cumple las siguientes propiedades:
- 0 ≤ P(A) ≤ 1
- P(E) = 1 y P(⌀) = 0
- $P(A) + P(\overline A) = 1$
- P(A ∪ B) = P(A) + P(B) − P(A ∩ B). Si A y B son icompatibles: P(A ∪ B) = P(A) + P(B)
Podemos extender el concepto de probabilidad a cualquier función que cumpla las propiedades anteriores.
Probabilidad condicionada
Puesto que la probabilidad está ligada al nivel de confianza sobre los resultados de un experimento, el hecho de que ocurra un suceso, puede cambiar la probabilidad de los demás. A esta nueva probabilidad se le llama condicionada
Ejemplo
Supongamos que tenemos una urna con 8 bolas numeradas pero de colores
blancos y negros de la cual se extrae una. Supongamos, también, que las
tres primeras son blancas y el resto negras, luego
E = {B1, B2, B3, N4, N5, N6, N7, N8}.
A priori, la
$P(\lbrace Sea\ impar\rbrace )=\frac{4}{8}=\frac{1}{2}$ por la
regla de Laplace. Tiene la misma probabilidad salir par que impar.
Vamos a suponer ahora que durante la extracción se percibe que la bola es blanca. La situación cambia, porque que sea blanca implica que hay 3 casos posibles y dos de las tres son impares. A esta nueva probabilidad se le llama condicionada y se denota así:
$P(I|B)=\dfrac{2}{3}$
La probabilidad de que sea impar ha aumentado por el hecho de haber
añadido la condición (o información) que es blanca.
Esta probabilidad la podemos transformar:
$P(I|B)=\dfrac{2}{3}=\dfrac{\dfrac{2}{8}}{\dfrac{3}{8}}=\dfrac{P(I\cap B)}{P(B)}$
Generalización del fórmula de la probabilidad condicionada
$P(A|B)=\dfrac{P(A\cap B)}{P(B)}$ y despejando:
P(A ∩ B) = P(A|B) ⋅ P(B)
Experimentos compuestos
Un experimento aleatorio compuesto es el que está formado por varios experimentos simples realizados de forma consecutiva.
Ejemplo:
Lanzar tres monedas, extraer cuatro cartas de una baraja, …
La probabilidad de un suceso compuesto se podrá calcular a partir de las probabilidades obtenidas de los experimentos simples usando la probabilidad condicional:
P(A ∩ B) = P(A) ⋅ P(B|A)
Independencia y dependencia de sucesos
Se dice que dos sucesos son independientes cuando la probabilidad de cada uno no depende del resultado del otro.
A y B son independientes ⇔ P(B|A) = P(B)
Ejemplos de sucesos independientes:
Lanzar varias monedas, extracción de varias cartas con reemplazamiento, sacar bolas de una urna con reemplazamiento, lanzar varios dados, …
Ejemplos de sucesos dependientes:
Extracción de varias cartas sin reemplazamiento, sacar bolas de una urna sin reemplazamiento, …
Cálculo de probabilidad compuesta para sucesos dependientes
Ejemplo:
En una urna hay tres bolas blancas y dos negras. Se extraen dos bolas sin reemplazamiento. Podemos construir el siguiente árbol con las probabilidades de los diferentes resultados:
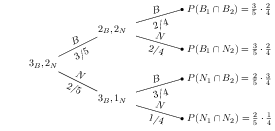
Ejemplos:
- Probabilidad de que las dos sean blancas: $P(B_1\cap B_2)=P(B_1)\cdot P(B_2|B_1)=\frac{3}{5}\cdot\frac{2}{4}=\frac{3}{10}$
- Probabilidad de que las dos sean negras: $P(N_1\cap N_2)=P(N_1)\cdot P(N_2|N_1)=\frac{2}{5}\cdot\frac{1}{4}=\frac{1}{10}$
- Probabilidad de que sean del mismo color: $P((B_1\cap B_2)\cup (N_1\cap N_2))=\frac{3}{10}+\frac{1}{10}=\frac{2}{5}$
Cálculo de probabilidad compuesta para sucesos independientes
Ejemplo:
En una urna hay tres bolas blancas y dos negras. Se extraen dos bolas con reemplazamiento. Ahora el árbol quedará:
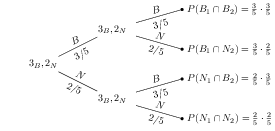
Ejemplos:
- Probabilidad de que las dos sean blancas: $P(B_1\cap B_2)=P(B_1)\cdot P(B_2|B_1)=\frac{3}{5}\cdot\frac{3}{5}=\frac{9}{25}$
- Probabilidad de que las dos sean negras: $P(N_1\cap N_2)=P(N_1)\cdot P(N_2|N_1)=\frac{2}{5}\cdot\frac{2}{5}=\frac{4}{25}$
- Probabilidad de que sean del mismo color: $P((B_1\cap B_2)\cup (N_1\cap N_2))=\frac{9}{25}+\frac{4}{25}=\frac{13}{25}$
Teorema de la probabilidad total
Ejemplo:
En un instituto de ESO hay 4 cursos: 1º, 2º, 3º y 4º. Se quiere estudiar la probabilidad de que un alumno del instituto esté con la gripe (Llamamos G al suceso tener gripe).
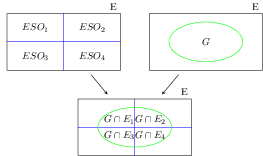
Como un alumno pertenece a un solo curso los sucesos ESO1 , ESO2, ESO3, y ESO4 (abreviados E1, etc.) son incompatibles. Además:
$G=(G \cap E_1)\cup(G \cap E_2)\cup(G \cap E_3)\cup(G \cap E_4)=\bigcup_{i=1}^4(G \cap E_i)$
Por tanto,
$P(G)=P(G \cap E_1)+P(G \cap E_2)+P(G \cap E_3)+P(G \cap E_4)=\sum_{i=1}^4 P(G \cap E_i)$
Aplicando la probabilidad condicionada:
$\begin{aligned} P(G)=P(E_1)\cdot P(G|E_1)+P(E_2)\cdot P(G|E_2)+\\+P(E_3)\cdot P(G|E_3)+P(E_1)\cdot P(G|E_4)= \\ =\sum_{i=1}^4 P(E_i)\cdot P(G|E_i)\end{aligned}$
Probabilidad total
Generalizando el resultado anterior:
Teorema de la probabilidad total:
Si A1, A2, …, An son sucesos incompatibles dos a dos y cuya unión es todo el espacio muestral, entonces la probabilidad de cualquier otro suceso B es:
$P(B)=\sum_{i=1}^n P(A_i)\cdot P(B|A_i)$
Ejemplo:
Tomando de nuevo el ejemplo de la urna en la que hay tres bolas blancas y dos negras. Si se extraen dos bolas, por ejemplo sin reemplazamiento, podemos calcular la probabilidad de que la segunda bola haya sido blanca:
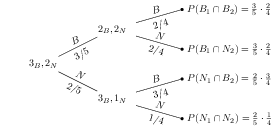
$P(B_2)=P(B_1)\cdot P(B_2|B_1) + P(N_1)\cdot P(B_2|N_1) = \frac{3}{5}\cdot\frac{2}{4} + \frac{2}{5}\cdot\frac{3}{4}$
Teorema de Bayes
Si A1, A2, …, An son sucesos incompatibles dos a dos y cuya unión es todo el espacio muestral, y B otro suceso cualquiera:
$P(A_i|B)=\dfrac{P(A_i \cap B)}{\sum_{i=1}^n P(A_i)\cdot P(B|A_i)}$
Demostración:
Por la probabilidad condicionada:
$P(A_i|B)=\dfrac{P(A_i \cap B)}{P(B)}$
Pero por la probabilidad total:
$P(B)=\sum_{i=1}^n P(A_i)\cdot P(B|A_i)$
Sustituyendo esta en la primera obtenemos el resultado
Ejemplo:
En el ejemplo del apartado anterior calcular la probabilidad de que la primera bola haya sido blanca si se sabe que la segunda ha sido blanca:
$P(B_1|B_2)=\dfrac{P(B_1 \cap B_2)}{P(B_1)\cdot P(B_2|B_1)+P(N_1)\cdot P(B_2|N_1)}=\dfrac{\dfrac{3}{5}\cdot\dfrac{2}{4}}{\dfrac{3}{5}\cdot\dfrac{2}{4} + \dfrac{2}{5}\cdot\dfrac{3}{4}}$
